- Accessibility Options:
- Skip to Content
- Skip to Search
- Skip to footer
- Office of Disability Services
- Request Assistance
- 305-284-2374
- Display:
- Default
- High Contrast
- Apply
- About UM
-
Schools
- School of Architecture
- College of Arts and Sciences
- Miami Herbert Business School
- School of Communication
- School of Education and Human Development
- College of Engineering
- School of Law
- Rosenstiel School of Marine, Atmospheric, and Earth Science
- Miller School of Medicine
- Frost School of Music
- School of Nursing and Health Studies
- The Graduate School
- Division of Continuing and International Education
- Alumni
- Roadmap
- 1: Introduction
- 2: Geography of the world ocean
- 3: Properties of seawater I
- 4: Properties of seawater II
- 5: Property distributions
- 6: Forcing of the Ocean
- 7: Conservation equations
- 8: Equations of Motion
- 9: Basin budgets
- 10: Scaling of the Equations of Motion
- 11: Ekman dynamics
- 12: Geostrophy
- 13: Potential vorticity equation
- 14: Sverdrup balance
- 15: Western Intensification
- 16: The Agulhas Current
- 17: Upwelling
- 18: Wind-generated waves
- 19: Eddies and planetary waves
- 20: Water mass formation
- 21: Abyssal circulation
- 22: Thermohaline circulation
- 23: Instrumentation and Experimentation
- 1: Introduction
- 2: Geography of the world ocean
- 3: Properties of seawater I
- 4: Properties of seawater II
- 5: Property distributions
- 6: Forcing of the Ocean
- 7: Conservation equations
- 8: Equations of Motion
- 9: Basin budgets
- 10: Scaling of the Equations of Motion
- 11: Ekman dynamics
- 12: Geostrophy
- 13: Potential vorticity equation
- 14: Sverdrup balance
- 15: Western Intensification
- 16: The Agulhas Current
- 17: Upwelling
- 18: Wind-generated waves
- 19: Eddies and planetary waves
- 20: Water mass formation
- 21: Abyssal circulation
- 22: Thermohaline circulation
- 23: Instrumentation and Experimentation




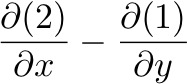
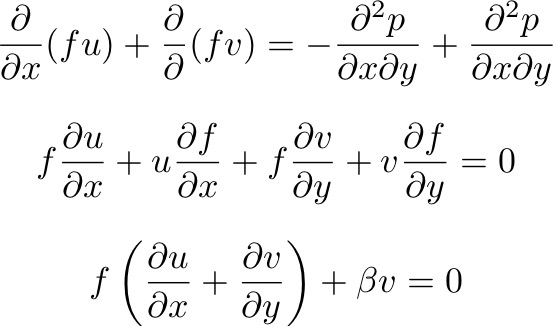
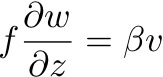
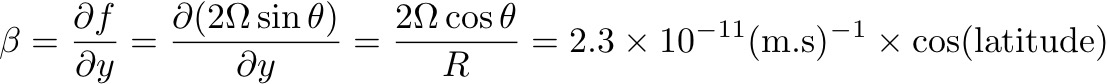
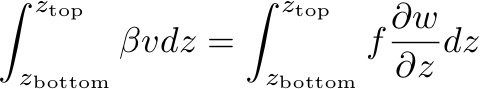


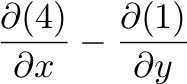

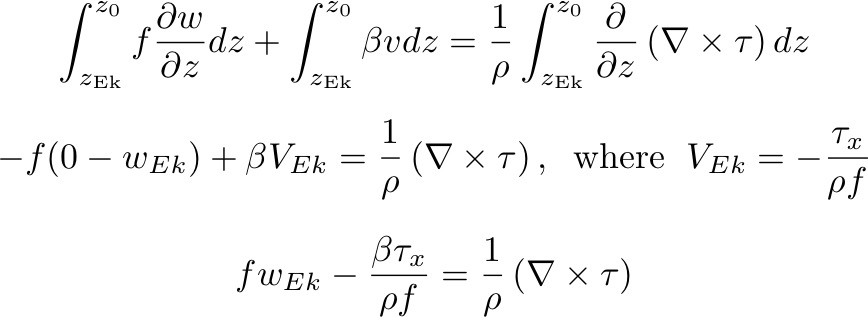
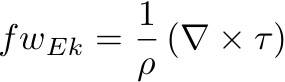
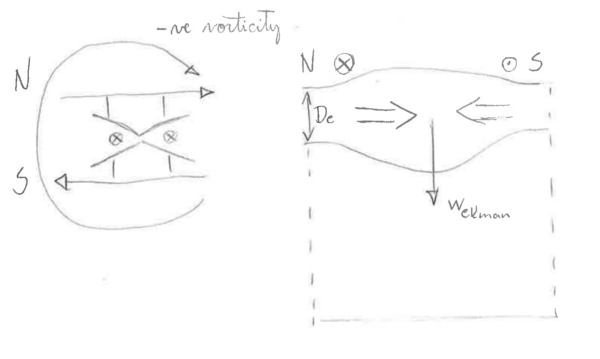

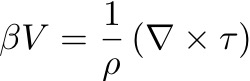
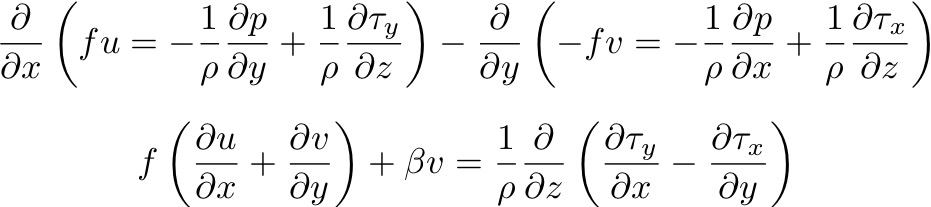 :
:
