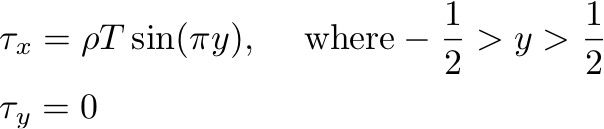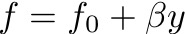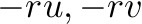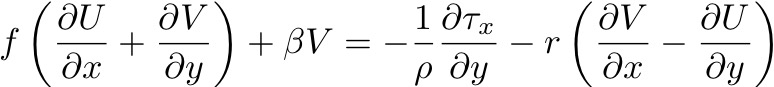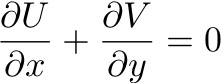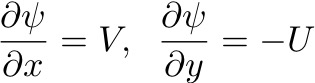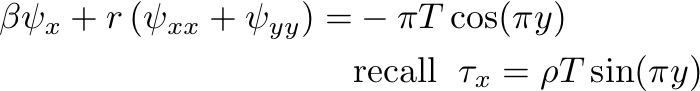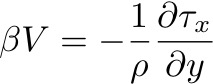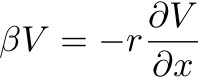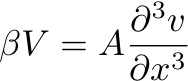Notes:
We have seen from the Sverdrup balance that, over the subtropical gyres of the northern hemisphere where the winds are cyclonic, the mid-ocean transport integrated top-to-bottom is southward. So, where/how does the southward mid-ocean flow return northward?
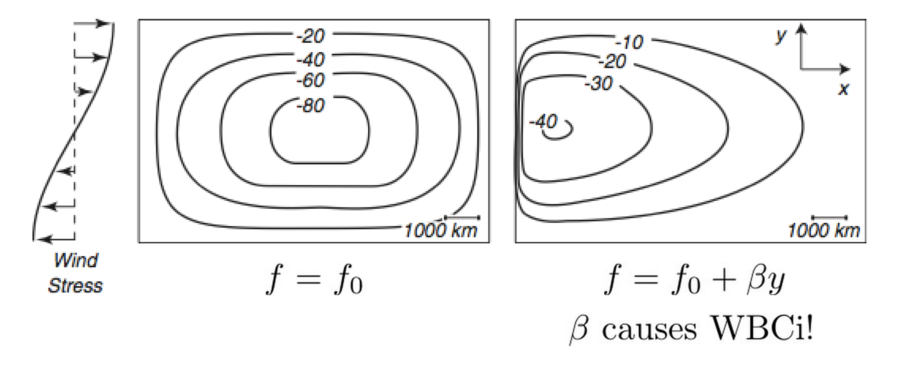
Henry Stommel addressed this problem and showed that the northward return flow occurs in a relatively narrow, strong current along the western boundary of an ocean basin. His theory has became known as "western intensification". All boundary currents of ocean gyres occur at the western boundaries, whether resulting from clockwise or counterclockwise winds or whether they are driven by thermohaline effects.
Stommel observed that strong currents like the Gulf Stream, the Kuroshio Current and the Agulhas Current are all at western boundaries. He set out to show why that should be, by using the equations of motion.
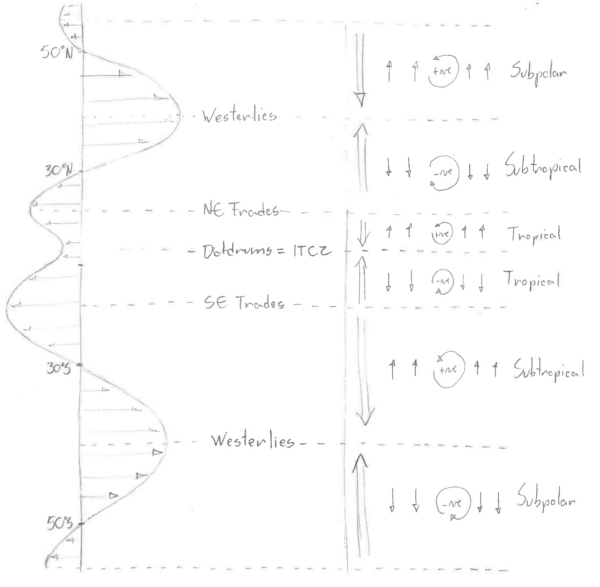
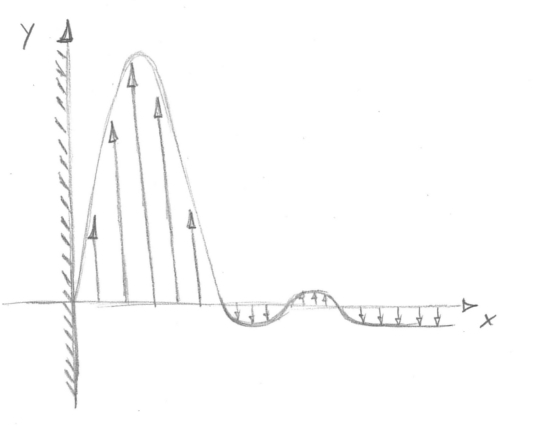
He considered a zonal wind stress that varied sinusoidally in the meridional direction - a simplified model of the winds over the subtropical gyres.
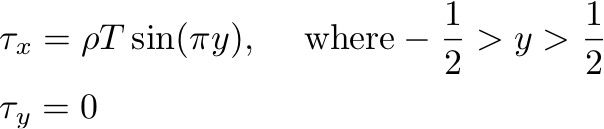
He included the β-effect:
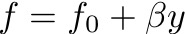
and added a simple frictional term, which acts contrary to the velocity:
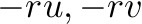
So the momentum equations become:

Just as Sverdrup did, Stommel eliminated the pressure term by cross-differentiating (1) and (2):

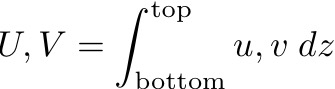
This looks just like the Sverdrup's equation, but with an extra friction term. Vertically integrating from top-to-bottom of the ocean, again as Sverdrup did, gives:
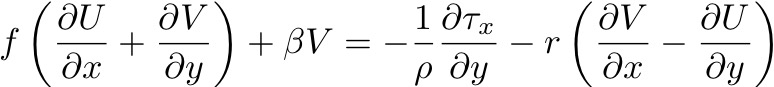
where U and V are the vertically integrated east and north velocity:
If we consider the WHOLE ocean, top to bottom, then the flow represented by U and V must be non-divergent. There can be no vertical velocity through the sea surface, or through the bottom of the ocean. Hence:
We can understand the western intensification in two ways:
1. We can consider that the interior flow is given by:
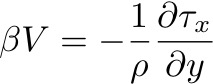
we know that V is southward everywhere and that this flow must "join" with a fictional boundary layer, where:
so that  , and as
, and as  then
then  .
.
Hence, for a boundary layer where the flow must be northward, V is positive and must decrease as x increases. Since r and β are always positive, the boundary layer must be on the western side of the basin.
Notice that the e-folding scale of the WBC is  . This is called the Stommel Boundary Layer.
. This is called the Stommel Boundary Layer.
 The Stommel boundary layer
The Stommel boundary layer
The boundary solution must join the interior flow:

and the total meridional flow across the basin is zero, since the transport in the boundary layer must be equal to the interior Sverdrup transport to respect continuity.
2. Second way to understand western intensification is to consider vorticity inputs and sinks:
- wind stress curl puts clockwise spin into the ocean;
- in the interior the flow is southward, effectively "storing" the spin;
- ultimately this water must return northward and lose its spin in order to once again join the interior flow;
- the ocean can only do this by obtaining anticlockwise spin via friction of a fast flow at the western boundary.
 North Atlantic subpolar gyre
North Atlantic subpolar gyre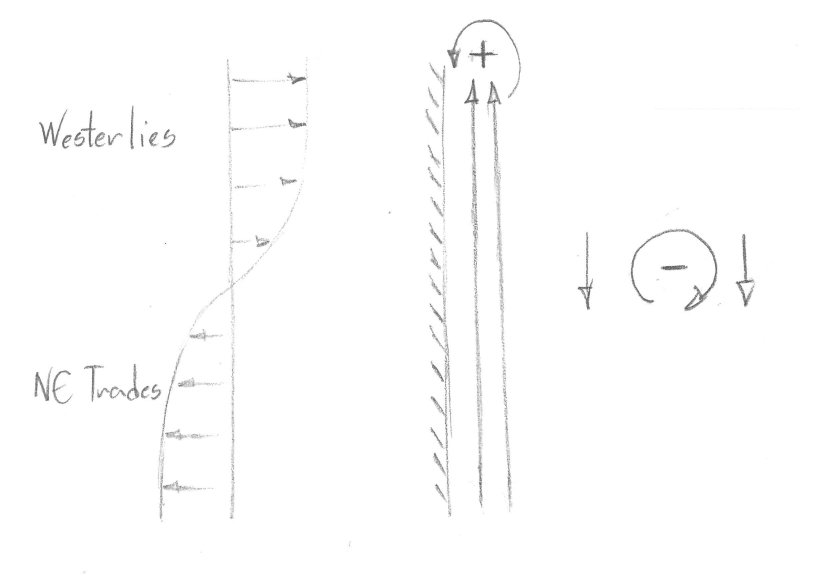 North Atlantic subtropical gyre
North Atlantic subtropical gyre South Atlantic subtropical gyreSo, the balance is:
South Atlantic subtropical gyreSo, the balance is:INPUT OF VORTICITY FROM WIND = FRICTIONAL DISSIPATION OF VORTICITY ALONG THE WESTERN BOUNDARY
Remember - the key element in western intensification is the beta effect. Because it is always positive, all strong flows end up on the western boundary.
With Sverdrup interior plus western intensification we can get the structure of the steady ocean circulation knowing the wind field.
Notice that for steady ocean circulation there is no meridional transport in the interior at latitudes of zero wind stress curl (or wind stress maximum). These latitudes define the gyre boundaries.
Many didn't like Stommel's simple friction, which is often thought of as a "bottom friction" because it acts on a nonsheared flow. Walter Munk re-examined the problem using "lateral" friction:

The form of the boundary layer is then derived by solving:
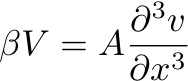
which yields a velocity profile which is zero (no slip) at the western boundary, a maximum in the boundary layer and decays quickly offshore, with small counter currents. This is called the Munk Boundary Layer.
The Munk boundary layer