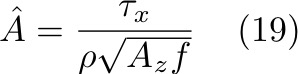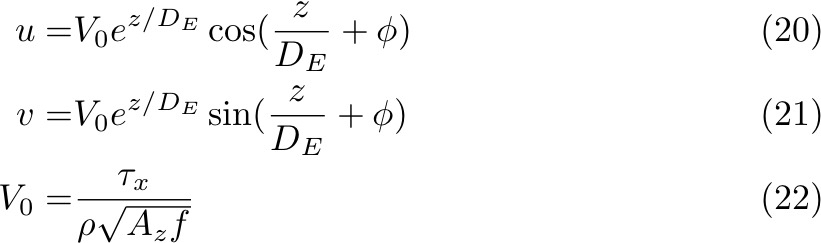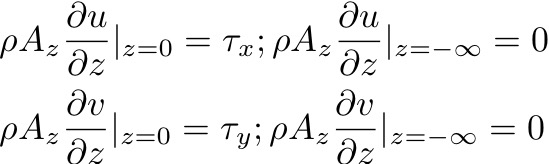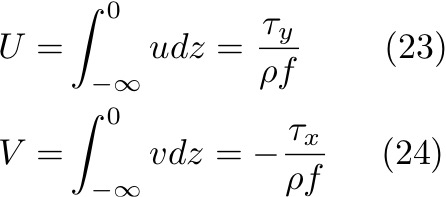Notes:
Nansen, in 1898, observed that icebergs moved at angles of between 30-30 degree to the right of the surface winds. He noticed this over many measurements, concluding that ocean currents were not the explanation. He argued that the balance between three forces exists:
- Wind Stress, W;
- Friction, D;
- Coriolis Force, C.
He later asked his colleagues Bjerknes to have a student working on a theoretical study of this problem: Ekman.
1. The Ekman Layer:
Ekman assumed STEADY, HOMOGENEOUS and horizontal flow with friction on a rotating Earth. Hence, the horizontal and time derivatives are zero.
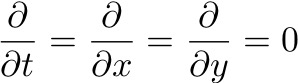
Leaves a balance between vertical friction and the Coriolis force:
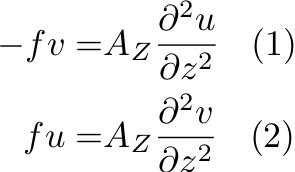
Ekman assumed that AZ is a constant throughout the boundary layer. Took following boundary conditions:
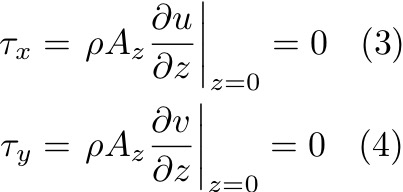
These equations are more complex to solve than the inertial equations, but Ekman used complex variables:
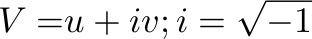
Multiply Equation (2) by i and add Equation (1):

Equation (7) has a solution of the general form:
Right away, we see that when 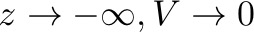 , and thus B = 0. In this case, V becomes:
, and thus B = 0. In this case, V becomes:
where 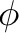 is the angle of the velocity to the wind. Now we need to separate the real and imaginary parts:
is the angle of the velocity to the wind. Now we need to separate the real and imaginary parts:
DE is the Ekman depth, and has unit of meters. It is a representative scale (e-folding scale) for the solution.
Substitue back to Equation (16):
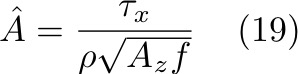
And the complete solutions of u and v:
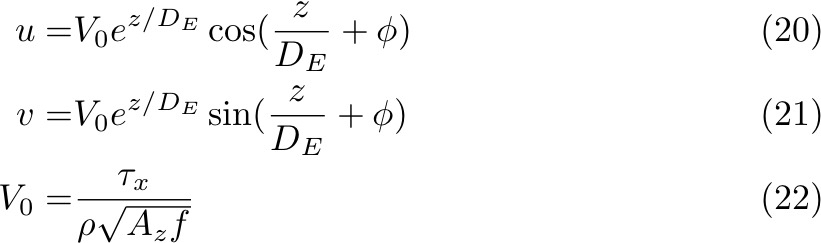
What does this solution look like? It's a spiral of currents that rotate and reduce with depth. Starting with surface velocities at 45° to the right of the wind. The e-folding scale is DE. Velocity vector rotates with "period" of 2πDE.

Ekman argued that the Ekman depth, a bottom of the Ekman layer, is where the velocity is in the opposite direction to velocity at the surface, which equals 2πDE.
In practice, it's very rare to observe an Ekman spiral, although some researchers have observed it by averaging over time. Ekman layer theory is oversimplified based on the following assumptions:
- No boundaries;
- Infinitely deep;
- AZ constant;
- Steady-state (wind and currents);
- No pressure gradient, no mixing, no waves;
- Homogeneous water;
- f-plane;
- Motions are horizontal.
The observed instantaneous surface currents can be 30° - 60° to the right of the wind. Maximenko and Niiler found that this angle varies as function of latitude. An explanation for this could be AZ and stratification. Another explanation is related to vertical variations of AZ, which is thought to grow linearly away from the sea surface.
2. Ekman Transport:
We go back to the balance of Equations (1) and (2), now with following boundary conditions at the surface and deep ocean:
If we vertically integrate these equations between z = 0 and z = -∞:
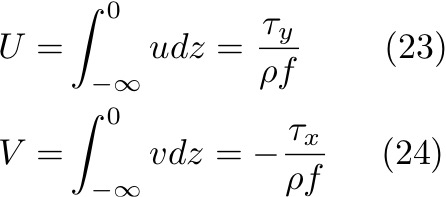
Which is the Ekman transport along the x and y directions. This is a very important result because the Ekman transport depends only on the wind stress and the Coriolis parameter. It does NOT depend on eddy viscosity or on the depth of the Ekman layer. Also, this result is valid even if the details of the Ekman spiral are not.
Note that for a wind stress in any direction the Ekman transport is 90° to the right in the Northern Hemisphere and 90° to the left in the Southern Hemisphere.
Last modified: Nov 2014



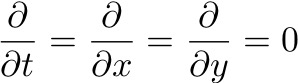
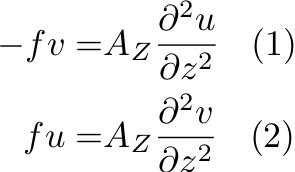
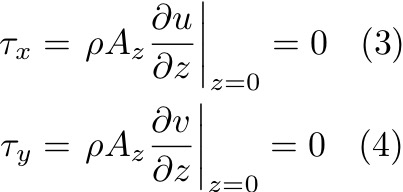
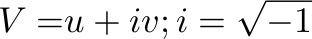

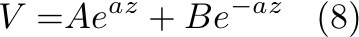
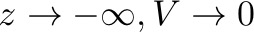

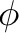 is the angle of the velocity to the wind. Now we need to separate the real and imaginary parts:
is the angle of the velocity to the wind. Now we need to separate the real and imaginary parts: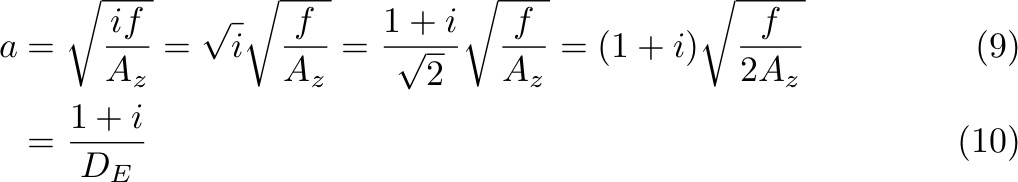
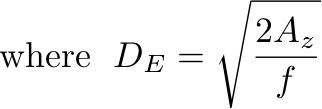

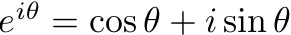 :
: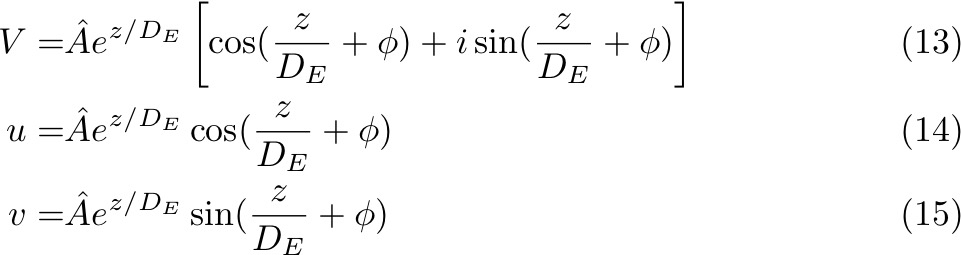
 and
and